Skip to content

Métodos y resultados

Método implementado

El método que se implementó para probar en este trabajo es \(KMeans\) para las MRIs en modo \(Flair\) y con variantes mencionadas anteriormente. Se utilizan las máscaras completas de tumores de la base de datos (no se separa según núcleos tumorales o edemas). Para el espacio de características se trabaja únicamente con los valores de intensidad de cada píxel.

Los pasos que conforman el algoritmo son los siguientes:

  1. Pre-procesamiento: Filtrado con \(BayeShrink\) y Corrección de Iluminación.
  2. KMeans (o variantes) para 4 clusters sobre cada slice.
  3. Determinación de región con tumor y líquido cefalorraquídeo en base a centroides.
  4. Etiquetado de subconjuntos 4-conectados en región asociada al tumor. Extracción de características.
  5. Detección y determinación de máscara del tumor en base a las características de cada subconjunto.

Para el paso 3, como criterio para extraer la región candidata a contener el tumor se utiliza tomar la región asociada al centroide de mayor valor de intensidad. Se toma esta decisión debido a que en el modo \(Flair\), debido al estado hipermetabólico de los tumores, las regiones tumorales se encuentran más iluminadas.

Para el paso 4 existen 2 variantes. Para la primera, el etiquetado de subconjuntos se realiza sobre cada slice, por lo que la extracción de características es de estructuras de dos dimensiones. Las características que se extraen en este caso son las siguientes:

  • Solidez
  • Circularidad
  • Área
  • Valor del centroide

En base a umbrales determinados experimentalmente sobre estas características se determina si existe un tumor o no en ese slice, y en caso de existir, se determina su subestructura asociada. En nuestro caso, los umbrales fueron 0.6 para la solidez, 0.2 para la circularidad, 200 para el área y 85 para el valor del centroide.

La segunda variante implica realizar el etiquetado sobre el volumen completo (extracción de características 3D). Las características que se extraen en este caso son las siguientes:

  • Solidez
  • Volumen
  • Intensidad media

Los umbrales seleccionados fueron 0.3 para la solidez, 6000 para el volumen y 95 para la intensidad media. Es pertinente mencionar que esta segunda variante se implementó sobre la variante de \(KMeans\) con el mejor desempeño para el primer tipo de etiquetado.

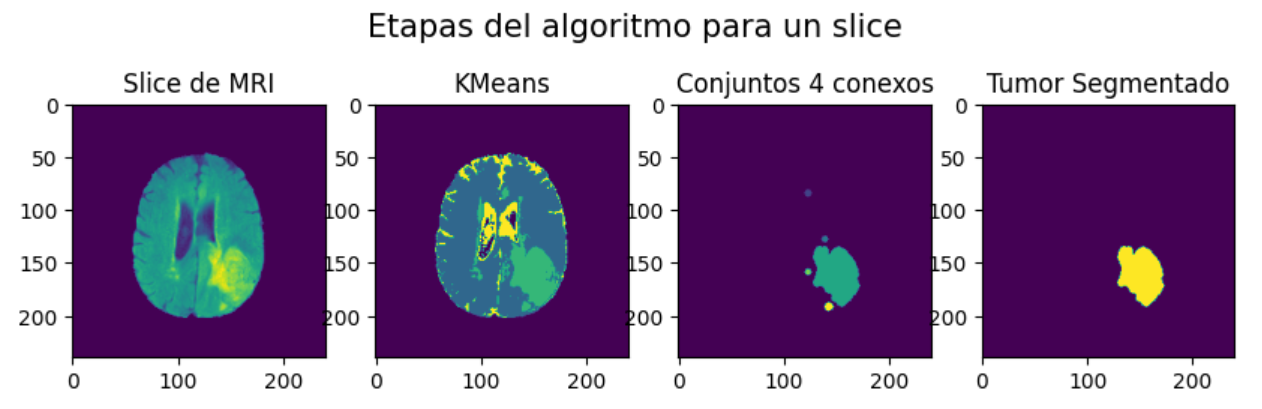
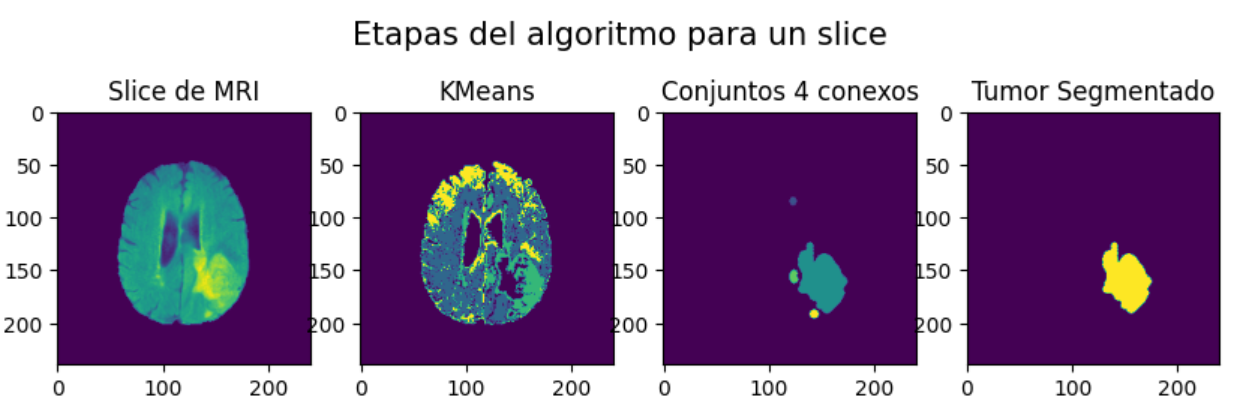
En las Figure 1 y Figure 2 se ilustran los pasos que sigue el algoritmo y una comparación entre \(KMeans\) Clásico y \(Fuzzy\).

Etapas del algoritmo clásico para un slice
Figure 1: Etapas del algoritmo clásico para un slice

Etapas del algoritmo fuzzy para un slice
Figure 2: Etapas del algoritmo fuzzy para un slice

Método Dice Hausdorff
KMeans- Etiquetado 2D 0.55 43.7
Fuzzy KMeans- Etiquetado 2D 0.57 41.2
KMeans- Etiquetado 3D 0.47 45.8

Es pertinente mencionar que luego de extraer el cluster de \(KMeans\) asociado al centroide de mayor intensidad se aplican algunas operaciones morfológicas como rellenado de conjuntos conexos y limpieza de partículas pequeñas. Esto fue especialmente útil para \(FuzzyKMeans\), que tendía devolver clusters más "salpicados" sobre toda la imagen.

Análisis de resultados

En esta sección se analizarán los resultados obtenidos y las posibles fuentes de error asociadas al desempeño.

Observando las MRI cuyos desempeños eran insatisfactorios para el etiquetado 2D, se concluyó que las principales fuentes de error son las siguientes:

  • Falsos positivos en slices
  • Tumores que conforman más de un conjunto 4 conexo
  • Tumores de baja circularidad ('con patas')

En las Figure 3 y Figure 4 se observan ejemplos que incluyen estas fuentes de error.

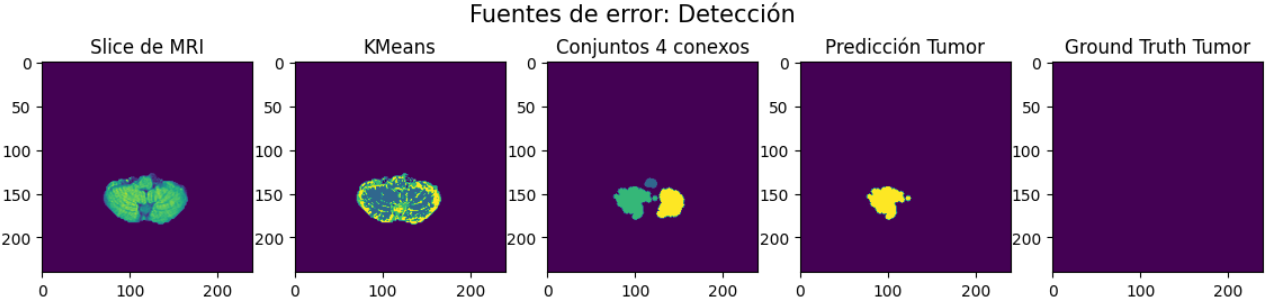
Errores de detección
Figure 3: Errores de detección

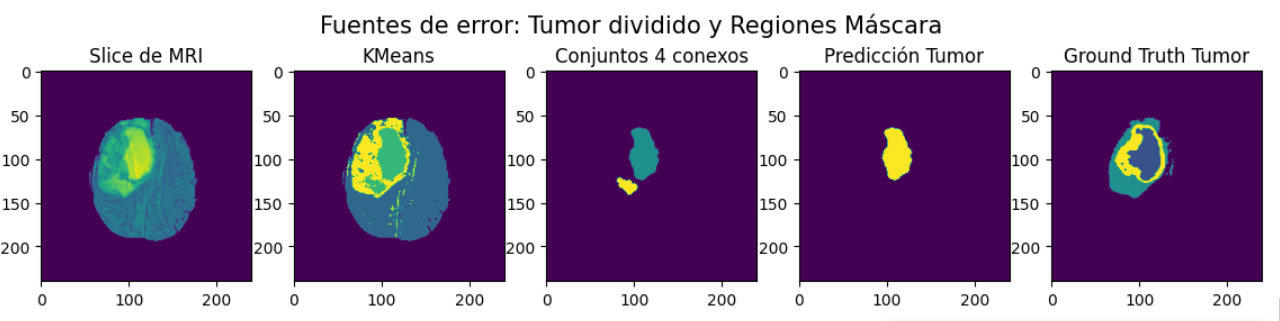
Errores, tumor en slice dividido en varias regiones
Figure 4: Errores, tumor en slice dividido en varias regiones

El tipo de error con mayores repercusiones al estar presente para casi todas las MRI es la presencia de falsos positivos en los primeros slices de las imágenes, ya que introduce grandes diferencias entre las máscaras generadas y las verdaderas. El umbral que incide directamente sobre la presencia de esta fuente de error es el del valor del centroide asociado a \(KMeans\). Sin embargo, se observó cualitativamente que en caso de imponer restricciones fuertes sobre el valor del umbral, aumenta la cantidad de falsos negativos en las máscaras.

Para el caso del etiquetado volumétrico, se detectan las siguientes fuentes de error:

  • Falsos positivos en primeros slices
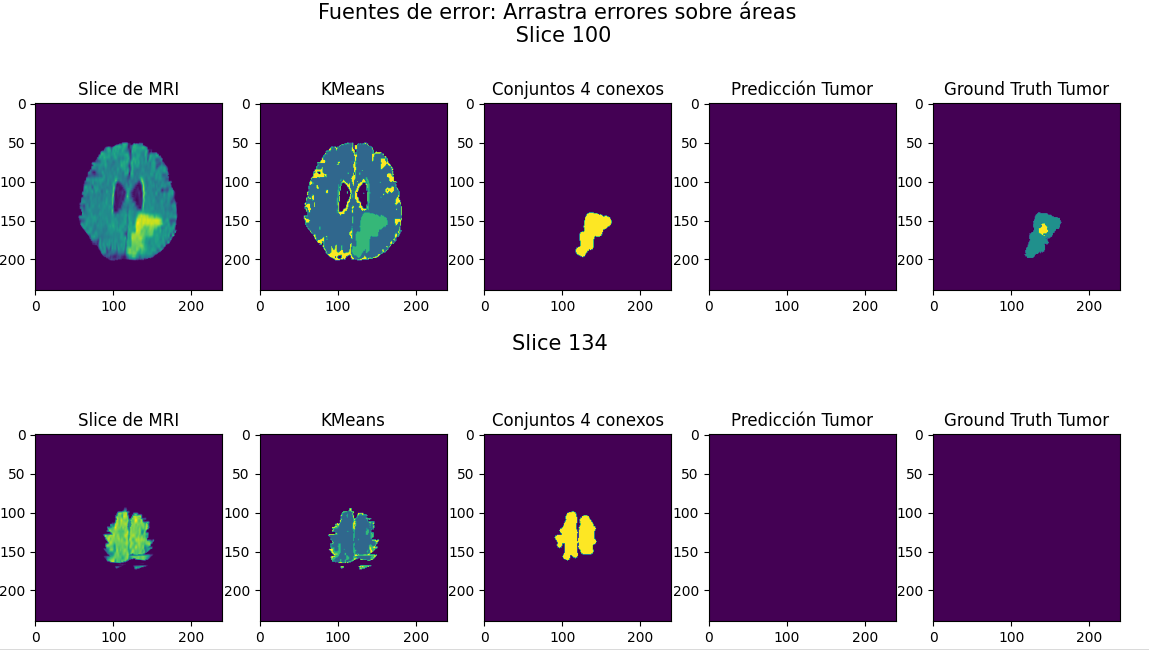
  • Arrastre de errores sobre primeros slices, repercusión sobre propiedades de las regiones

Se mantiene entonces la presencia de estos falsos positivos con el agregado de que al etiquetar sobre los volúmenes, si hay superposición de estos falsos positivos sobre los slices, es posible que la región final que contenga el tumor además tenga estos agregados, lo cual distorsiona las propiedades de la región y vuelve más difícil la determinación de los umbrales. En la siguiente Figure 5 se observa el arrastre de errores para 2 slices de una MRI.

Es pertinente mencionar que el etiquetado sobre volúmenes elimina una fuente de error asociada al etiquetado en áreas, los tumores que se encuentran separados en 2 regiones conexas en algunas slices. Esto sucede ya que al etiquetar sobre volúmenes, si existen puntos de superposición de estas regiones separadas a una región común en slices contiguos, se identifica una estructura única que contiene ambas regiones.

Arrastre de errores en volumen
Figure 5: Arrastre de errores en volumen

Estrategias de Mejora

Debido al alcance del proyecto y las demoras en tiempos de ejecución de los algoritmos, se dificulta realizar varias pruebas sobre el conjunto de datos. Sin embargo, es posible pensar diferentes estrategias que logren mitigar algunas de las causas de error. Algunas estrategias posibles son las siguientes:

  • Búsqueda de umbrales óptimos algorítmicamente \(\rightarrow\) En vez de fijar umbrales cualitativamente, hacer una búsqueda aleatoria sobre umbrales posibles.
  • Combinación de predictores (\(Fuzzy\) + \(Clásico\)) \(\rightarrow\) Extraer beneficios de ambos algoritmos.
  • Combinación de métodos de etiquetado \(\rightarrow\) Análisis de propiedades de regiones conexas en 2D combinado con análisis en regiones conexas en 3D. Se pueden descartar la pertenencia de slices al volumen según ciertas características.
  • Aprovechar otras modalidades de MRI \(\rightarrow\) Ciertas modalidades pueden ser mejores para determinar regiones específicas de los tumores.
  • Imponer restricciones de continuidad sobre las máscaras en cada slice \(\rightarrow\) En muchos casos varía la máscara de forma discontinua, lo cual es poco plausible.

Comparación de resultados

A continuación se realiza una breve comparación de resultados y reflexión de las diferencias entre los métodos de Deep Learning y clásicos. La Figure 6 contiene los resultados obtenidos por el método ganador 1 de la competencia de Brats 2018. El resultado relevante es el de la fila del medio, que representa Whole tumor. Por otra parte, en la subsección anterior se presentaron los resultados de las mismas métricas para el método clásico implementado en este proyecto.

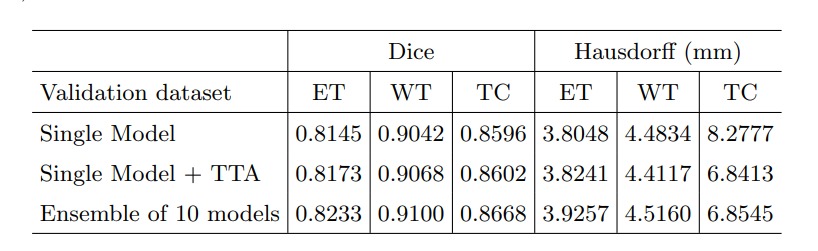
Resultados del método presentado por @brats_1.
Figure 6: Resultados del método presentado por @brats_1.

Observando el desempeño es fácil ver que el método de Deep Learning tiene una performance muy superior al método clásico. De todas formas, no es menor tener en cuenta que del método clásico se conoce el criterio de aceptación de un vóxel como tumor. Esto brinda una cuota de interpretabilidad que es muy importante en casos de aplicación médicos. Al implementar el método se sabe que la decisión toma en cuenta valores de intensidad en imágenes MRI, la circularidad de los objetos detectados y su tamaño, tres elementos que son intuitivos, tienen justificación médica, y son medibles. Por otro lado, en los métodos de Deep Learning, la decisión es completamente dependiente de la red y las etiquetas, y uno tiene poco control o intuición sobre el resultado.

3D Slicer

En esta etapa del proyecto también se evaluó la herramienta de visualización y procesamiento de imágenes médicas 3D Slicer. La herramienta permite observar todas las vistas del cerebro a distintas profundidades como se puede ver en la Figure 7, y además obtener una vista 3D del mismo.

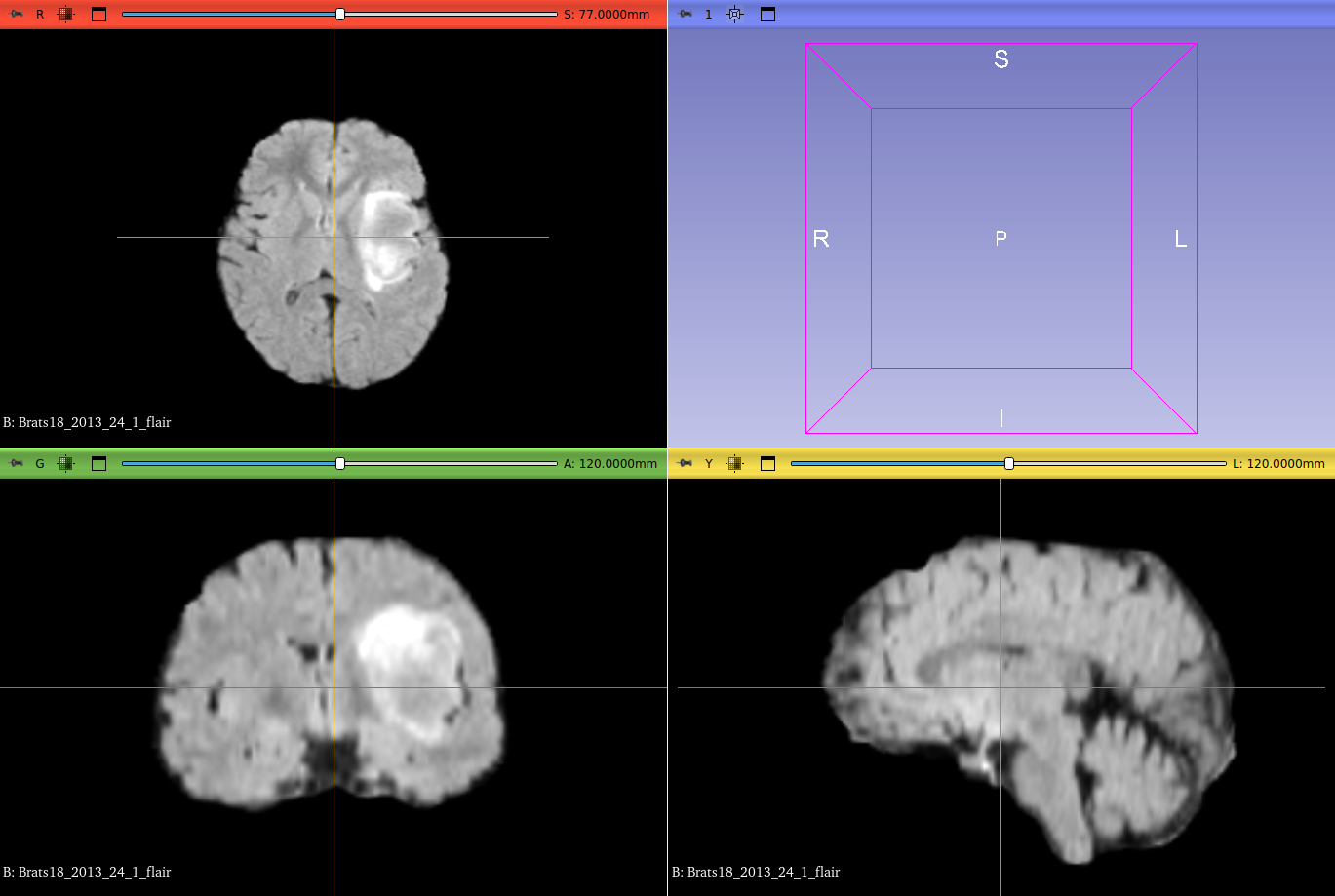
Vistas del MRI de un sujeto de BraTs 2018 en 3D Slicer
Figure 7: Vistas del MRI de un sujeto de BraTs 2018 en 3D Slicer

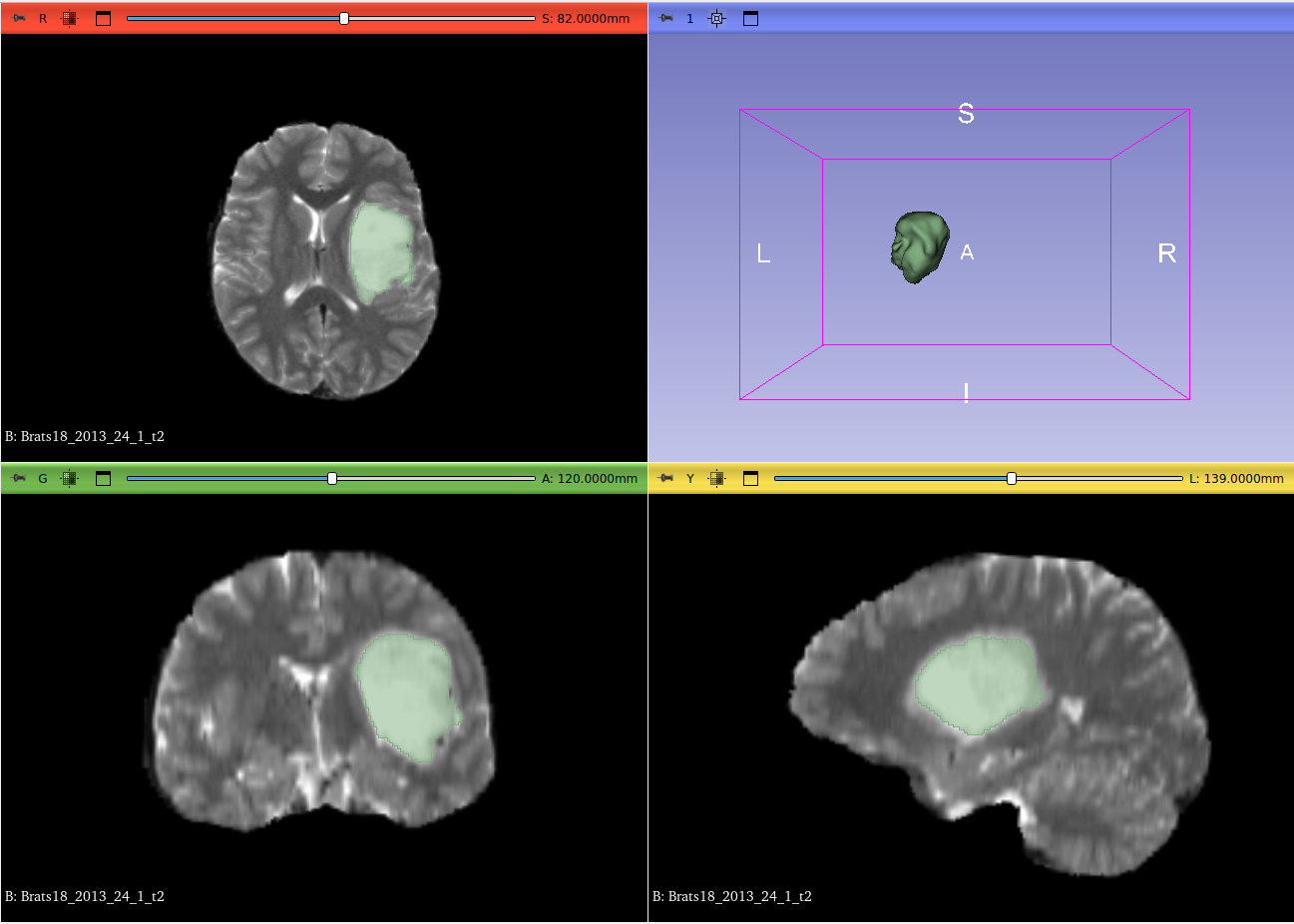
De manera más relevante, 3D Slicer tiene sus propias herramientas de segmentación 3D, tanto manuales, como asistidas y completamente independientes. Uno de los métodos clásicos más destacados es uno de Region Growing asistido. Para utilizarlo, se debe seleccionar una semilla y una región aproximada donde se encuentra el tumor y luego inicializar el modelo, que proveerá una segmentación 3D inicial que luego se puede refinar manualmente y suavizar con otras herramientas del Slicer. En la Figure 8 se puede ver la inicialización del método seleccionada por el usuario y en la Figure 9 se puede visualizar la segmentación hallada luego del Region Growing en uno de los ejemplos del dataset de Brats 2018. El resultado final además se puede editar con una herramienta de lápiz, y suavizar. La región marcada en verde en cada plano (axial, sagital y coronal) es la que se visualiza en el 3D, desde la perspectiva axial.

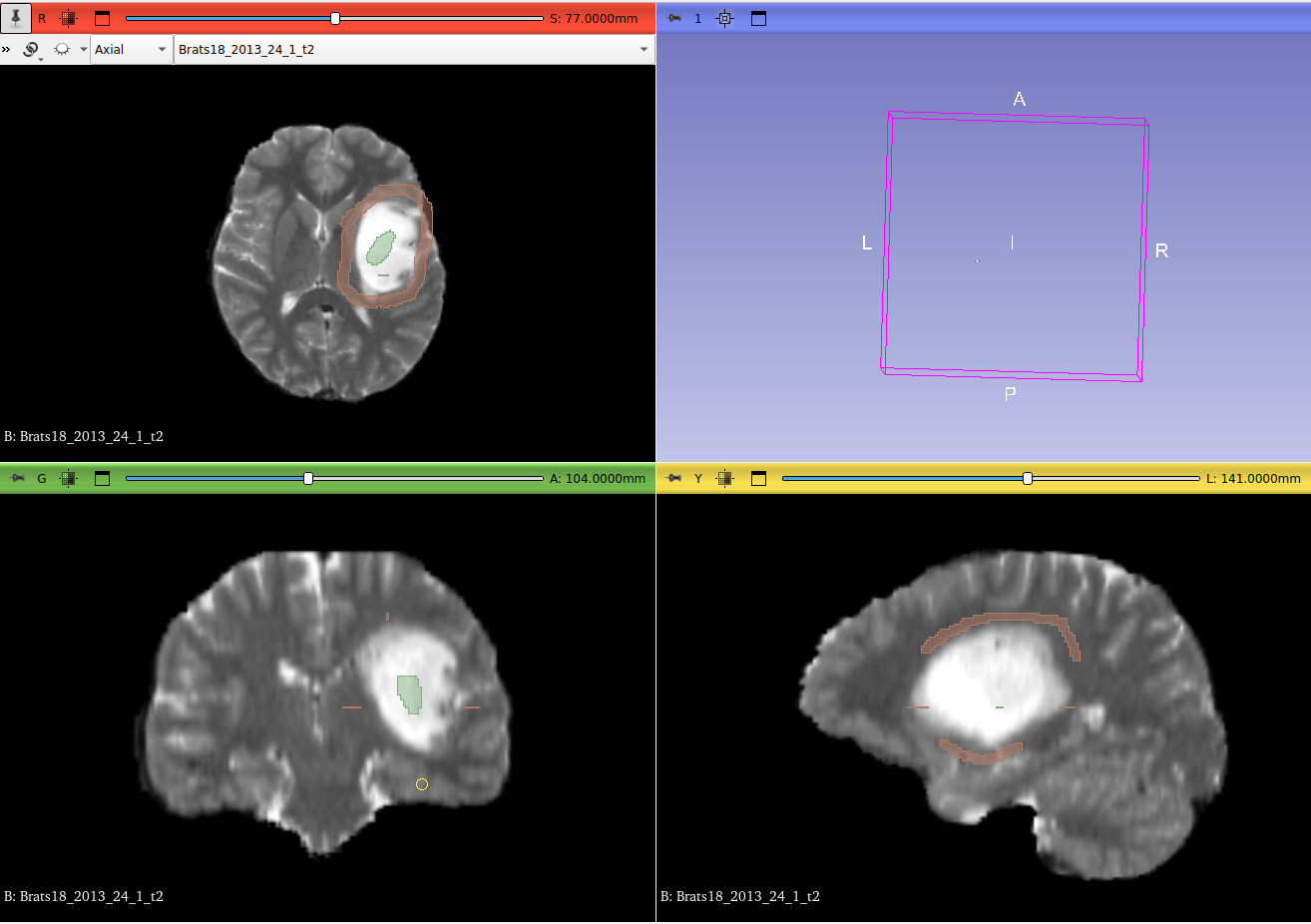
Semilla de inicialización del método de crecimiento de regiones.
Figure 8: Semilla de inicialización del método de crecimiento de regiones.

Tumor segmentado por método de crecimiento de regiones.
Figure 9: Tumor segmentado por método de crecimiento de regiones.

Por último, esta herramienta permite descargar módulos de segmentación de desarrolladores externos entre los cuales hay algunos módulos de Deep Learning como por ejemplo MonAI 2 y Total Segmentation 3.

  1. Andriy Myronenko. 3d MRI brain tumor segmentation using autoencoder regularization. CoRR, 2018. URL: http://arxiv.org/abs/1810.11654, arXiv:1810.11654. ↩

  2. M. Jorge Cardoso, Wenqi Li, Richard Brown, Nic Ma, Eric Kerfoot, Yiheng Wang, Benjamin Murrey, Andriy Myronenko, Can Zhao, Dong Yang, Vishwesh Nath, Yufan He, Ziyue Xu, Ali Hatamizadeh, Andriy Myronenko, Wentao Zhu, Yun Liu, Mingxin Zheng, Yucheng Tang, Isaac Yang, Michael Zephyr, Behrooz Hashemian, Sachidanand Alle, Mohammad Zalbagi Darestani, Charlie Budd, Marc Modat, Tom Vercauteren, Guotai Wang, Yiwen Li, Yipeng Hu, Yunguan Fu, Benjamin Gorman, Hans Johnson, Brad Genereaux, Barbaros S. Erdal, Vikash Gupta, Andres Diaz-Pinto, Andre Dourson, Lena Maier-Hein, Paul F. Jaeger, Michael Baumgartner, Jayashree Kalpathy-Cramer, Mona Flores, Justin Kirby, Lee A. D. Cooper, Holger R. Roth, Daguang Xu, David Bericat, Ralf Floca, S. Kevin Zhou, Haris Shuaib, Keyvan Farahani, Klaus H. Maier-Hein, Stephen Aylward, Prerna Dogra, Sebastien Ourselin, and Andrew Feng. Monai: an open-source framework for deep learning in healthcare. 2022. URL: https://arxiv.org/abs/2211.02701, arXiv:2211.02701. ↩

  3. Jakob Wasserthal, Hanns-Christian Breit, Manfred T. Meyer, Maurice Pradella, Daniel Hinck, Alexander W. Sauter, Tobias Heye, Daniel T. Boll, Joshy Cyriac, Shan Yang, Michael Bach, and Martin Segeroth. Totalsegmentator: robust segmentation of 104 anatomic structures in ct images. Radiology: Artificial Intelligence, September 2023. URL: http://dx.doi.org/10.1148/ryai.230024, doi:10.1148/ryai.230024. ↩