Skip to content

Revisión de la literatura

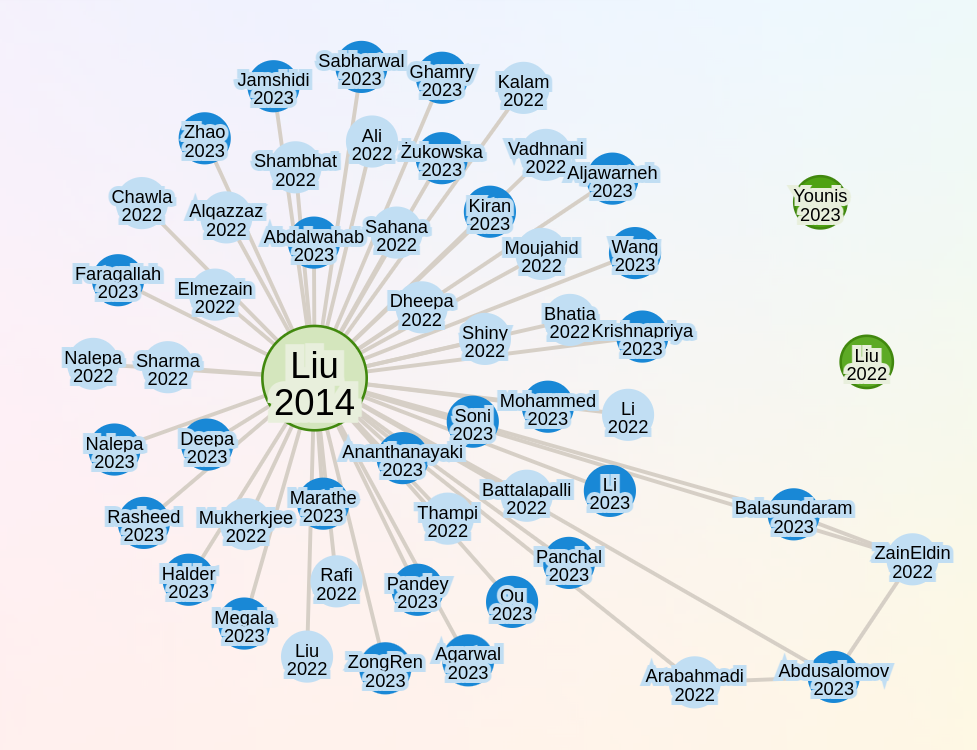
Uno de los papers de referencia para comenzar la lectura es una revisión de Liu et. al. 1 que comprende métodos en 2D (imágenes) y métodos volumétricos. Estos últimos son los centrales para nuestra investigación. En la Figure 1 se puede visualizar el grafo de citas a este paper. El propósito de esta visualización es poder descubrir nuevos artículos relacionados al tema que hayan tomado este survey como referencia. Los que efectivamente hayan sido seleccionados para este trabajo serán referenciados más adelante.

En particular, el artículo de Liu et. al. 1 parece relevante en un contexto en el que la mayoría del resto de los surveys más actuales solo revisan la literatura de Deep Learning y no métodos clásicos. A continuación se presenta un overview de los distintos métodos que parecen más relevantes y una sección referida a los modelos de Deep Learning.

Grafo creado por Research Rabbit de artículos relacionados al survey de Liu et. al.
Figure 1: Grafo creado por Research Rabbit de artículos relacionados al survey de Liu et. al.

Métodos basados en regiones

Los métodos basados en regiones más usuales son los de crecimiento de regiones a partir de una semilla (Region growing methods) 2. Un gran beneficio es que son fácilmente generalizables a datos volumétricos, y de hecho existe mucha literatura que los utiliza en el problema de segmentación volumétrica 3456. Estos métodos, de manera general, siguen los siguientes pasos:

  1. Selección de una semilla \( s \), i.e., un pixel o voxel inicial. Se puede utilizar como una oportunidad para tener un método semi-supervisado en que un usuario elige la semilla, o se puede hacer de manera aleatoria.
  2. Se define un criterio de similitud entre elementos.
  3. Se agregan elementos a la semilla bajo el criterio de similitud, terminando en una región \( R_1 \).
  4. También hay que definir un criterio de similitud entre una región y un elemento.
  5. Agregar a \( R_1 \) los píxeles vecinos que cumplen el criterio de similitud, resultando en una región \( R_2 \supset R_1 \).
  6. Continuar el proceso hasta que no hayan píxeles vecinos que cumplan el criterio de similitud.

Para imágenes en escala de grises, el criterio de similitud en general es sobre la diferencia de intensidades en valor absoluto, con una pequeña tolerancia. El caso 3D podría generalizar a lo mismo simplemente con el valor del voxel, o utilizar una construcción más compleja con ambos volúmenes T1 y T2.

Representación visual de un método de crecimiento de regiones
Figure 2: Representación visual de un método de crecimiento de regiones

Más en profundidad, se proponen variaciones de los métodos de crecimiento de regiones clásicos que tratan de resolver algunos de los problemas usuales con ellos. Un ejemplo es el desarrollado por S. Lakare et. al 3, que ataca el problema de el efecto de volumen parcial (partial volume effect). Este efecto se define como la pérdida de actividad aparente en los vóxeles de los bordes debido a la resolución limitada del sistema de imágenes 3. Es decir, la distinción de intensidad entre clases de tejidos en el borde se difumina, porque el vóxel puede representar más de un tipo de tejido. Para contrarrestar este problema, S. Lakare et. al proponen una que asser M. Salman 4 prueba sobre el mismo problema que se plantea en este trabajo. Esencialmente, el nuevo método llamado Modified region growing method (MRGM) incorpora la información de los gradientes para poder detectar los bordes con más precisión en una etapa posterior a una primera versión de la segmentación utilizando crecimiento de regiones clásico.

Finalmente, el último conjunto de métodos discutidos dentro de los métodos basados en detección de regiones son los llamados watershed 578. Los métodos de watershed se basan en la analogía de la superficie de una imagen con las cuencas hidrográficas. Se basa en tratar los valores de intensidad de los píxeles como alturas en un relieve topográfico. En este contexto, los píxeles de baja intensidad representan los valles, y los de alta intensidad, las crestas. La segmentación se realiza "llenando" estos valles con agua, que sube uniformemente hasta que se encuentra con las aguas de otros valles en las crestas, formando así las fronteras naturales entre diferentes regiones de la imagen.

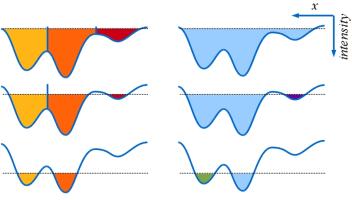
Representación visual del método de watershed
Figure 3: Representación visual del método de watershed

Más formalmente, la estructura del método es:

  1. Selección de semilla: Se eligen puntos iniciales o semillas para las regiones.
  2. Crecimiento de regiones: se agrega a los píxeles vecinos a la región, siguiendo caminos de bajo gradiente, hasta que encuentran barreras de alto gradiente que detienen su crecimiento.
  3. Detección de fronteras: La agregación de píxeles continúa hasta que las regiones llenadas desde diferentes marcadores se encuentran en altos gradientes, definiendo así las fronteras de las regiones.
  4. Finalización: El proceso se completa cuando toda la imagen ha sido segmentada y todas las regiones están claramente delimitadas por barreras naturales.

El problema que tratan de resolver muchos de los artículos que profundizan en este método es la sobre-segmentación 578.

Classification and clustering methods

Los métodos de clasificación y clusterización buscan segmentar la imagen en regiones (o \(clusters\)) con el objetivo de maximizar la similitud intra-cluster y la distancia inter-cluster. Un algoritmo que es protagónico en este tipo de métodos es \(KMeans\) y sus posibles variaciones.

En el caso de \(KMeans\), la estructura que vincula los píxeles en base a sus características dentro de una región son los centroides. Estos consisten en un punto en el espacio de características determinado por los píxeles. Cada píxel se vincula a un centroide bajo el criterio de minimizar la distancia píxel-centróide total en el espacio de características.

La estructura básica del algoritmo consiste en: 1. Inicialización de centroides 2. Actualización de pertenencias de píxeles a las regiones determinadas por cada centroide 3. Actualización de centroides 4. Se repiten los pasos 2. y 3. hasta que prácticamente no varía la posición de los centroides, la distancia entre píxeles y centroides alcanza un mínimo pre-definido o se llega a un máximo de iteraciones.

Algunas de las variantes del algoritmo principal son \(FuzzyKMeans\) y \(Rough-FuzzyKMeans\). Para la primera, en vez de trabajar con regiones determinísticas, se asignan probabilidades de pertenencia a las regiones para cada píxel dentro de la imagen. Esto es ventajoso ya que en el caso de imágenes biomédicas permite la posibilidad de superposiciones de tejidos. La última es una fusión entre el algoritmo clásico y la variante anterior en la cual se determinan 2 regiones del cluster, una determinística y otra probabilística. En base a criterios de distancia se determina cuales píxeles pertenecen a cada una de las regiones. También se diferencia el cálculo de los centróides en base a esta pertenencia.

En la literatura existen diferentes elecciones del espacio de características en el cual se trabaja. La opción más simple es simplemente trabajar con la intensidad asociada a cada píxel. Existen otras opciones que trabajan con un espacio constituido por el píxel y su ubicación, o por regiones de píxeles asociadas a un pixel 'protagonista'.

Detección de anomalías

El artículo de Prastawa et al. 9 presenta un marco para la segmentación automática de tumores cerebrales basado en la detección de anomalías que se centra en tres etapas principales:

  1. Detección de regiones anómalas:

    • Utiliza un atlas cerebral registrado como modelo de cerebros sanos.
    • Las regiones con características de intensidad que se desvían de las esperadas para un cerebro sano son identificadas como anómalas.
    • Se emplea una estimación robusta de los parámetros de intensidad para eliminar los valores atípicos y obtener las distribuciones de intensidad para las diferentes clases de tejido cerebral sano.

  2. Detección de edema y tumor:

    • Se determina si las regiones anómalas contienen tumor y/o edema.
    • Las intensidades de la imagen T2 se utilizan para identificar el edema, ya que este generalmente aparece más brillante debido a su alto contenido de líquido.
    • Se aplica una técnica de clustering no supervisada para diferenciar entre tumor y edema en las regiones anómalas.

  3. Aplicación de restricciones geométricas y espaciales:

    • Se utilizan restricciones geométricas y espaciales para refinar la segmentación inicial de tumor y edema.
    • El tumor se considera una estructura con forma "blobby" (grumosa), y el edema debe estar conectado espacialmente al tumor.
    • La segmentación se revalida iterativamente para mejorar la precisión utilizando estas restricciones.

Deformable Models

La idea central de los Deformable Models es que el modelo inicial, que puede ser una curva, una superficie o una malla, se deforma gradualmente para coincidir con las características del objeto en la imagen (o superficie). En definitiva, son una representación matemática que se adapta dinámicamente a la estructura del objeto de interés. Estos modelos pueden modificar su forma y posición en respuesta a ciertas fuerzas o restricciones derivadas de los datos de imagen 1011.

Las componentes claves de un son el modelo inicial (que no significa que sea asistido como en el caso de region growing): una forma básica que se ajustará para coincidir con la estructura objetivo; la Energía Interna que representa la resistencia del modelo a cambios abruptos de forma, asegurando suavidad y continuidad; y la Energía Externa que "guía" el modelo hacia los contornos del objeto de interés. Finalmente, se tienen en cuenta ambas energías para minimizar una función de costo que ajuste el modelo a los datos. En la Tabla 1 se encuentra una breve descripción de los principales Deformable Models en la literatura 1213.

Tipo Definición Energía Interna Por qué Deformable
Snakes Curvas que se mueven en una imagen para encontrar bordes. Mantiene la curva suave y sin cambios abruptos. La curva se deforma y adapta a los contornos del objeto mientras minimiza la función de energía total.
Conjuntos de nivel Contornos representados como el conjunto de nivel de una función de mayor dimensión. Mantiene la superficie suave y coherente. La superficie puede cambiar de forma y adaptarse a cambios topológicos como la fusión y división de regiones.
Deformable Templates Formas predefinidas que se deforman para coincidir con el objeto de interés. Basada en la estadística de las variaciones de forma, típicamente utilizando PCA. La plantilla se ajusta dinámicamente a la forma del objeto utilizando tanto conocimiento previo como datos actuales de la imagen.
Finite Element Representación en malla donde los nodos se mueven según leyes físicas. Basada en las propiedades biomecánicas del tejido, asegurando deformaciones realistas. La malla se deforma en respuesta a fuerzas externas mientras mantiene características físicas realistas.

Tabla 1: Comparación de diferentes tipos de Deformable Models en la segmentación de tumores cerebrales en 3D

En imágenes médicas en particular, modelos deformables bidimensionales y tridimensionales se utilizan para segmentar, visualizar, rastrear y cuantificar una variedad de estructuras anatómicas que varían en escala desde lo macroscópico hasta lo microscópico 13. En particular, el artículo de McInerney et. al. 13 refieren a los Deformable Models como una herramienta para segmentar volúmenes médicos que asegura más robustez y suavidad en las soluciones.

Uno de los principales artículos referenciados en el tema es el de Khotanlou et. al. 14 donde se presenta un modelo que tiene una fase de segmentación del cerebro completo, y luego se detecta el tumor, basado en estudio de simetrías y fuzzy classification. El primer método se basa en la suposición de que el tumor aparece en la imagen con niveles de gris específicos, correspondientes a una clase adicional. El segundo método asume que el cerebro es aproximadamente simétrico en forma, y que los tumores pueden detectarse como áreas que se desvían de la simetría al observar los niveles de gris. Esta detección proporciona la inicialización para un paso de segmentación más preciso, realizado en la segunda etapa, utilizando un modelo deformable paramétrico restringido por relaciones espaciales difusas.

El modelo de fluido cargado (CFM) 15 para la segmentación de imágenes médicas utiliza una analogía física donde elementos cargados, distribuidos a lo largo del contorno inicial del objeto, generan un campo eléctrico calculado mediante la ecuación de Poisson. Estos elementos se repelen entre sí y se deforman en respuesta al campo eléctrico y al gradiente de la imagen, ajustando el contorno hacia los bordes del objeto a segmentar. El proceso iterativo alterna entre la distribución de carga y la deformación del frente, moviendo los elementos del contorno según las fuerzas calculadas hasta que el contorno se estabiliza en los límites del objeto, proporcionando una segmentación precisa y robusta, incluso en estructuras complejas y en 3D.

Métodos de Deep Learning

Con el auge de los modelos de Deep Learning 16 en la década de los 2010s, también surgieron modelos que procesaran datos en 3D. Las primeras redes procesaban datos tanto en vóxeles 1718 utilizando convoluciones 3D, como en formato de nubes de puntos 19 (2016), diseñando un método nuevo e innovador que permitía trabajar directamente con los puntos de datos. VoxNet y 3D ShapeNets, por ejemplo, demostraron cómo las redes neuronales convolucionales pueden aplicarse a representaciones volumétricas para tareas como la clasificación de objetos. PointNet revolucionó el campo al manejar directamente las nubes de puntos sin necesidad de una representación volumétrica intermedia, simplificando y mejorando el procesamiento. Al observar la altísima superación en performance de los modelos de Deep Learning por sobre los métodos clásicos (como los nombrados en las secciones anteriores), de la mano con estos avances, se empiezan a implementar soluciones para segmentar imágenes médicas, destacando modelos como el Efficient Multi-Scale 3D CNN 20, que combina escalas múltiples y Conditional Random Field (CRF) para segmentación de lesiones cerebrales; la 3D U-Net 21, que adapta la exitosa U-Net a datos volumétricos, y V-Net 22, diseñado específicamente para la segmentación de imágenes médicas volumétricas. Como ejemplo de arquitectura para tener una representación visual, se puede ver la []{fig:cnn_3d}. Se identifica una arquitectura de encoder-decoder que disminuye y luego aumenta la dimensión de la imagen para hacer la segmentación utilizando una U-NET con convoluciones en 3D.

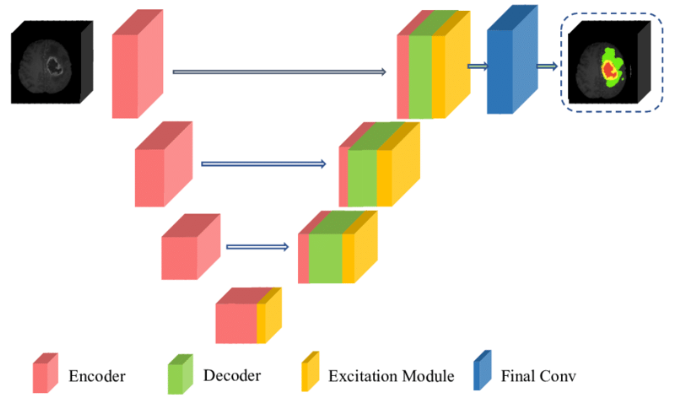
Arquitectura ejemplo de CNN 3D
Figure 4: Arquitectura ejemplo de CNN 3D

Como en todas las áreas donde se involucra el Deep Learning, los avances tecnológicos son muy rápidos y desde el surgimiento de estos modelos 3D han surgido muchísimos otros, de los cuales solo incluiremos algunos de los más relevantes en materia de segmentación 3D de tumores en este reporte. Dado que el Multimodal Brain Tumor Segmentation Challenge (BraTs) es una competencia muy relevante en esta área y muchas de las soluciones son de código abierto, se le da hincapié a estas sobre los muchísimos trabajos que ofrecen soluciones de redes de código cerrado y que por lo tanto no son reproducibles 232425. En este contexto, se presenta la Tabla 2 que contiene un resumen de algunos de los métodos publicados que fueron ganadores de BraTs.

Red Propuesta Se basa en Descripción
ED + VAE 26 Utiliza una red de segmentación semántica basada en una arquitectura de encoder-decoder con una rama adicional de autoencoder variacional (VAE). Este método, presentado por Andriy Myronenko, utiliza una red de segmentación semántica basada en una arquitectura de encoder-decoder con una rama adicional de autoencoder variacional (VAE). La rama VAE se utiliza para reconstruir las imágenes de entrada durante el entrenamiento, lo que ayuda a regularizar el codificador al agrupar mejor las características en el punto final del codificador. Esto mejora significativamente el rendimiento de la segmentación, especialmente en presencia de datos de entrenamiento limitados. La otra rama de decoder segmenta el tumor. El método ganó el primer lugar en el desafío BraTS 2018.
3D U-Net 27 Desarrollado por Feifan Wang et. al., este método emplea una arquitectura 3D U-Net para la segmentación de tumores cerebrales. Desarrollado por Feifan Wang et. al., este método emplea una arquitectura 3D U-Net para la segmentación de tumores cerebrales. Se utilizan estrategias de normalización y segmentación por parches, que permiten manejar mejor las variaciones en las imágenes de diferentes pacientes. La arquitectura 3D U-Net es eficaz para capturar el contexto volumétrico de las MRI, mejorando la precisión de la segmentación de las diferentes subregiones del tumor. Este enfoque también se probó en el desafío BraTS 2019, obteniendo buenos resultados en las métricas de evaluación.
3D U-Net Ensemble 28 Utiliza un conjunto de modelos de redes U-Net. Propuesto en el artículo por Th´eophraste et. al., este enfoque utiliza un conjunto de modelos de redes U-Net. Cada modelo en el ensemble se entrena de manera independiente y sus predicciones se combinan para mejorar la robustez y precisión del resultado final. Este método aprovecha la diversidad de los modelos individuales para reducir el riesgo de sobreajuste y mejorar la generalización. Este método mostró mejoras significativas en la segmentación de tumores en el desafío BraTS 2020.
nnU-Net 29 Método de segmentación que se configura automáticamente para cualquier nueva tarea en el dominio biomédico. Incluye preprocesamiento, arquitectura de red, entrenamiento y post-procesamiento. Desarrollado por Fabian Isensee y sus colegas, nnU-Net es un método de segmentación que se configura automáticamente para cualquier nueva tarea en el dominio biomédico. Incluye preprocesamiento, arquitectura de red, entrenamiento y post-procesamiento. Utiliza un conjunto de parámetros fijos, basados en reglas y empíricos para adaptarse rápidamente a nuevas tareas. nnU-Net demostró ser altamente eficaz y superó a la mayoría de los enfoques especializados existentes en 23 conjuntos de datos públicos (incluído BraTs) utilizados en competiciones internacionales de segmentación biomédica.
nnU-Net Revisited 30 Introduce variantes nnU-Net ResEnc (Residual Encoder) y diferentes tamaños para adaptarse a varios presupuestos de VRAM (M, L, XL); buscando mejorar la eficiencia de adaptación y el rendimiento en conjuntos de datos específicos. La versión revisitada del nnU-Net introduce variantes nnU-Net ResEnc (Residual Encoder) y diferentes tamaños para adaptarse a varios presupuestos de VRAM (M, L, XL); buscando mejorar la eficiencia de adaptación y el rendimiento en conjuntos de datos específicos. Además, enfatiza la importancia de la validación rigurosa, identificando y evitando los errores comunes de validación que pueden llevar a conclusiones erróneas sobre el rendimiento de los métodos.

Tabla 2: Métodos de Segmentación de Tumores Cerebrales

Los ganadores de las ediciones que se encuentran en la tabla no son de código abierto y las diferencias de performance son marginales. Lo mismo sucede con los ganadores más nuevos.

  1. Jin Liu, Min Li, Jianxin Wang, Fangxiang Wu, Tianming Liu, and Yi Pan. A survey of mri-based brain tumor segmentation methods. Tsinghua Science and Technology, 19(6):578–595, 2014. doi:10.1109/TST.2014.6961028. ↩↩

  2. M. Jourlin. Chapter two - various contrast concepts. In Michel Jourlin, editor, Logarithmic Image Processing: Theory and Applications, volume 195 of Advances in Imaging and Electron Physics, pages 27–60. Elsevier, 2016. URL: https://www.sciencedirect.com/science/article/pii/S1076567016300325, doi:https://doi.org/10.1016/bs.aiep.2016.04.002. ↩

  3. Mie Sato, S. Lakare, Ming Wan, A. Kaufman, and M. Nakajima. A gradient magnitude based region growing algorithm for accurate segmentation. In Proceedings 2000 International Conference on Image Processing (Cat. No.00CH37101), volume 3, 448–451 vol.3. 2000. doi:10.1109/ICIP.2000.899432. ↩↩↩

  4. Yasser M. Salman. Modified technique for volumetric brain tumor measurements. Journal of Biomedical Science and Engineering, 2009. URL: https://www.scirp.org/pdf/jbise%20vol.2%20no.1-02-01-20090714092941.pdf#page=20, doi:10.4236/jbise.2009.21003. ↩↩

  5. Saif D. Salman and Ahmed A. Bahrani. Segmentation of tumor tissue in gray medical images using watershed transformation method. Int. J. Adv. Comp. Techn., 2:123–127, 2010. URL: https://api.semanticscholar.org/CorpusID:15623618. ↩↩↩

  6. Hiroyuki Sekiguchi, Koichi Sano, and Tetsuo Yokoyama. Interactive 3-dimensional segmentation method based on region growing method. Systems and Computers in Japan, 25(1):88–97, 1994. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/scj.4690250108, arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1002/scj.4690250108, doi:https://doi.org/10.1002/scj.4690250108. ↩

  7. Joshua E. Cates, Ross T. Whitaker, and Greg M. Jones. Case study: an evaluation of user-assisted hierarchical watershed segmentation. Medical Image Analysis, 9(6):566–578, 2005. ITK. URL: https://www.sciencedirect.com/science/article/pii/S1361841505000320, doi:https://doi.org/10.1016/j.media.2005.04.007. ↩↩

  8. E. Dam, M. Loog, and M. Letteboer. Integrating automatic and interactive brain tumor segmentation. In Proceedings of the 17th International Conference on Pattern Recognition, 2004. ICPR 2004., volume 3, 790–793 Vol.3. 2004. doi:10.1109/ICPR.2004.1334647. ↩↩

  9. Marcel Prastawa, Elizabeth Bullitt, Sean Ho, and Guido Gerig. A brain tumor segmentation framework based on outlier detection. Medical Image Analysis, 8(3):275–283, 2004. Medical Image Computing and Computer-Assisted Intervention - MICCAI 2003. URL: https://www.sciencedirect.com/science/article/pii/S1361841504000295, doi:https://doi.org/10.1016/j.media.2004.06.007. ↩

  10. Chenyang Xu and Jerry L. Prince. 10 - gradient vector flow deformable models. In ISAAC N. BANKMAN, editor, Handbook of Medical Imaging, Biomedical Engineering, pages 159–169. Academic Press, San Diego, 2000. URL: https://www.sciencedirect.com/science/article/pii/B978012077790750014X, doi:https://doi.org/10.1016/B978-012077790-7/50014-X. ↩

  11. Thomas Albrecht, Marcel Lüthi, and Thomas Vetter. Deformable Models, pages 210–215. Springer US, Boston, MA, 2009. URL: https://doi.org/10.1007/978-0-387-73003-5_88, doi:10.1007/978-0-387-73003-5_88. ↩

  12. S. Kevin Zhou and D. Xu. Chapter 8 - a probabilistic framework for multiple organ segmentation using learning methods and level sets. In S. Kevin Zhou, editor, Medical Image Recognition, Segmentation and Parsing, The Elsevier and MICCAI Society Book Series, pages 157–178. Academic Press, 2016. URL: https://www.sciencedirect.com/science/article/pii/B9780128025819000081, doi:https://doi.org/10.1016/B978-0-12-802581-9.00008-1. ↩

  13. Tim McInerney and Demetri Terzopoulos. Deformable models in medical image analysis: a survey. Medical Image Analysis, 1(2):91–108, 1996. URL: https://www.sciencedirect.com/science/article/pii/S1361841596800077, doi:https://doi.org/10.1016/S1361-8415(96)80007-7. ↩↩↩

  14. Hassan Khotanlou, Olivier Colliot, Jamal Atif, and Isabelle Bloch. 3d brain tumor segmentation in mri using fuzzy classification, symmetry analysis and spatially constrained deformable models. Fuzzy Sets and Systems, 160(10):1457–1473, 2009. Special Issue: Fuzzy Sets in Interdisciplinary Perception and Intelligence. URL: https://www.sciencedirect.com/science/article/pii/S0165011408005368, doi:https://doi.org/10.1016/j.fss.2008.11.016. ↩

  15. Herng-Hua Chang and Daniel J. Valentino. An electrostatic deformable model for medical image segmentation. Computerized Medical Imaging and Graphics, 32(1):22–35, 2008. URL: https://www.sciencedirect.com/science/article/pii/S0895611107001322, doi:https://doi.org/10.1016/j.compmedimag.2007.08.012. ↩

  16. Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. Nature, 521(7553):436–444, 2015. URL: https://doi.org/10.1038/nature14539, doi:10.1038/nature14539. ↩

  17. Daniel Maturana and Sebastian Scherer. Voxnet: a 3d convolutional neural network for real-time object recognition. In Ieee/rsj International Conference on Intelligent Robots and Systems, 922–928. 2015. ↩

  18. Zhirong Wu, Shuran Song, Aditya Khosla, Xiaoou Tang, and Jianxiong Xiao. 3d shapenets for 2.5d object recognition and next-best-view prediction. CoRR, 2014. URL: http://arxiv.org/abs/1406.5670, arXiv:1406.5670. ↩

  19. Charles Ruizhongtai Qi, Hao Su, Kaichun Mo, and Leonidas J. Guibas. Pointnet: deep learning on point sets for 3d classification and segmentation. CoRR, 2016. URL: http://arxiv.org/abs/1612.00593, arXiv:1612.00593. ↩

  20. Konstantinos Kamnitsas, Christian Ledig, Virginia F. J. Newcombe, Joanna P. Simpson, Andrew D. Kane, David K. Menon, Daniel Rueckert, and Ben Glocker. Efficient multi-scale 3d CNN with fully connected CRF for accurate brain lesion segmentation. CoRR, 2016. URL: http://arxiv.org/abs/1603.05959, arXiv:1603.05959. ↩

  21. Özgün Çiçek, Ahmed Abdulkadir, Soeren S. Lienkamp, Thomas Brox, and Olaf Ronneberger. 3d u-net: learning dense volumetric segmentation from sparse annotation. CoRR, 2016. URL: http://arxiv.org/abs/1606.06650, arXiv:1606.06650. ↩

  22. Fausto Milletari, Nassir Navab, and Seyed-Ahmad Ahmadi. V-net: fully convolutional neural networks for volumetric medical image segmentation. CoRR, 2016. URL: http://arxiv.org/abs/1606.04797, arXiv:1606.04797. ↩

  23. Xinyu Zhou, Xuanya Li, Kai Hu, Yuan Zhang, Zhineng Chen, and Xieping Gao. Erv-net: an efficient 3d residual neural network for brain tumor segmentation. Expert Systems with Applications, 170:114566, 2021. URL: https://www.sciencedirect.com/science/article/pii/S0957417421000075, doi:https://doi.org/10.1016/j.eswa.2021.114566. ↩

  24. Dongwei Liu, Ning Sheng, Yutong Han, Yaqing Hou, Bin Liu, Jianxin Zhang, and Qiang Zhang. Scau-net: 3d self-calibrated attention u-net for brain tumor segmentation. Neural Computing and Applications, 35(33):23973–23985, 2023. URL: https://doi.org/10.1007/s00521-023-08872-8, doi:10.1007/s00521-023-08872-8. ↩

  25. Hiba Mzoughi, Ines Njeh, Ali Wali, Mohamed Ben Slima, Ahmed BenHamida, Chokri Mhiri, and Kharedine Ben Mahfoudhe. Deep multi-scale 3d convolutional neural network (cnn) for mri gliomas brain tumor classification. Journal of Digital Imaging, 33(4):903–915, August 2020. URL: https://doi.org/10.1007/s10278-020-00347-9, doi:10.1007/s10278-020-00347-9. ↩

  26. Andriy Myronenko. 3d MRI brain tumor segmentation using autoencoder regularization. CoRR, 2018. URL: http://arxiv.org/abs/1810.11654, arXiv:1810.11654. ↩

  27. Feifan Wang, Runzhou Jiang, Liqin Zheng, Chun Meng, and Bharat Biswal. 3D U-Net Based Brain Tumor Segmentation and Survival Days Prediction, pages 131–141. Springer International Publishing, 2020. URL: http://dx.doi.org/10.1007/978-3-030-46640-4_13, doi:10.1007/978-3-030-46640-4_13. ↩

  28. Theophraste Henry, Alexandre Carre, Marvin Lerousseau, Theo Estienne, Charlotte Robert, Nikos Paragios, and Eric Deutsch. Brain tumor segmentation with self-ensembled, deeply-supervised 3d u-net neural networks: a brats 2020 challenge solution. 2020. URL: https://arxiv.org/abs/2011.01045, arXiv:2011.01045. ↩

  29. Fabian Isensee, Paul F. Jaeger, Simon A. A. Kohl, Jens Petersen, and Klaus H. Maier-Hein. Nnu-net: a self-configuring method for deep learning-based biomedical image segmentation. Nature Methods, 18(2):203–211, 2021. URL: https://doi.org/10.1038/s41592-020-01008-z, doi:10.1038/s41592-020-01008-z. ↩

  30. Fabian Isensee, Tassilo Wald, Constantin Ulrich, Michael Baumgartner, Saikat Roy, Klaus Maier-Hein, and Paul F. Jaeger. Nnu-net revisited: a call for rigorous validation in 3d medical image segmentation. 2024. URL: https://arxiv.org/abs/2404.09556, arXiv:2404.09556. ↩